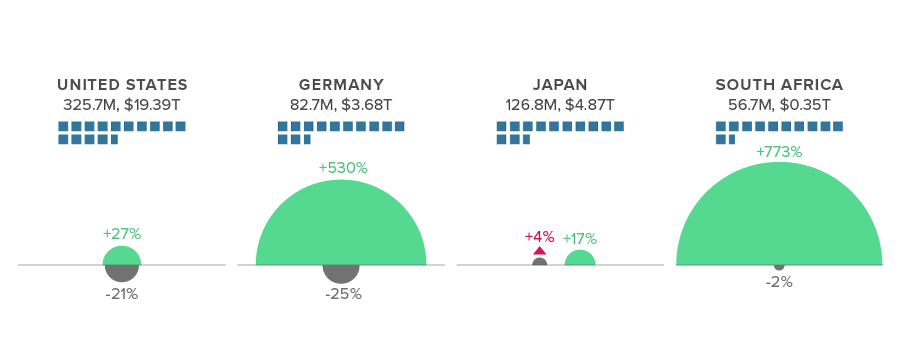
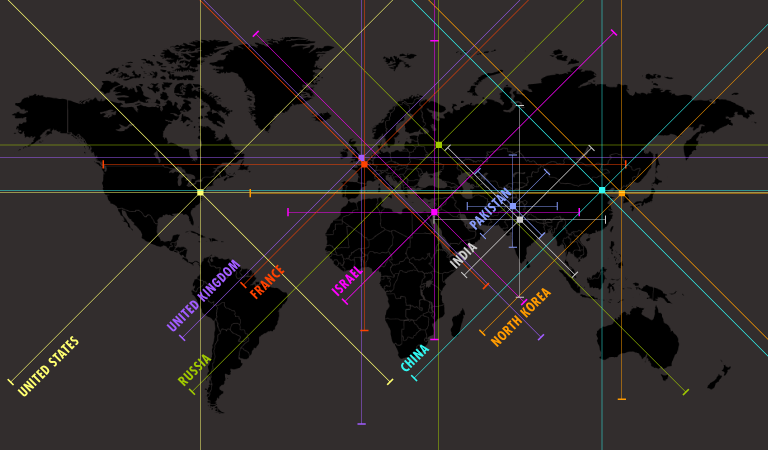
Podcasts are a great way to further your knowledge of social enterprise and international development topics even when you don’t have a lot of time on your hands. We picked a few of our favorites that provide a variety of perspectives on the state of the world from policy analysts, think-tank leaders, journalists, and more.